Word Embeddings: A Story

Computers are dumb. “Hold up... You, a computer scientist, are saying that computers are dumb?” Yes. They are dumb. At their core, they only execute simple operations on binary data and that’s about it. From adding numbers to translating sentences, it’s all just simple operations on binary data. “But how is it even possible to operate on textual data?” Good question! Let’s find out.

Introduction

Data can come in different forms like audio, images, text, etc. In order for the computer to process data, it needs to represent it in a format it can understand.  Audio is easy. It is a one-dimensional array of numbers. Each number represents the amplitude of the signal at a particular time.

Images are also easy. They are two-dimensional arrays of numbers. Each number represents the grayscale value for that particular pixel.

What about text? Well, there is no explicit numerical representation for text as for audio and images, but we can come up with one ourselves. One way of representing each sentence, for example, would be by using a one-dimensional array with a length equal to the length of our vocabulary. At each position, we store the number of times a unique word from the vocabulary appeared in the sentence. “Mmm… OK.” — you seem confused. Let me give you an example.

Let’s say that our vocabulary consists of the following words: [ and, get, is, see, you, what ]. We can represent the sentence:

what you see is what you get

as follows:

[ 0, 1, 1, 1, 2, 2 ]

This is a perfectly valid representation that scientists call the bag-of-words representation. 

It has several drawbacks though. First, the arrays are large because of the size of the vocabularies. Second, the arrays are sparse. Sentences don’t usually contain all the words in the vocabulary; so we need to come up with a better approach, one that would:

Generate short dense arrays, and;

Encode information in the arrays.

“What type of information can we encode?”— you ask. Well, we can encode the meaning of the sentence. If we treat these arrays as points in space, sentences that are semantically similar will appear close to each other. “That is cool, but why do we need to encode such information?” Raw data is more difficult to operate with. The end goal of all this is to make the machine learning task as easy as possible. Imagine that you are an ML engineer at Twitter and you want to develop a system for filtering mean tweets. Generating representations for tweets that encode such information is going to make the problem a lot easier to solve.

Do you want to learn how we encode this information? “Yes!”— you shout. Well, buckle up, because this is going to be a mathsy section.

Factorization

As you already know, for any machine learning algorithm to work we need DATA. For generating textual representations we need textual data (duh!). But we are lucky because there is an abundance of textual data on the internet. Take Wikipedia for example, with millions and millions of articles. Now, how do we proceed?

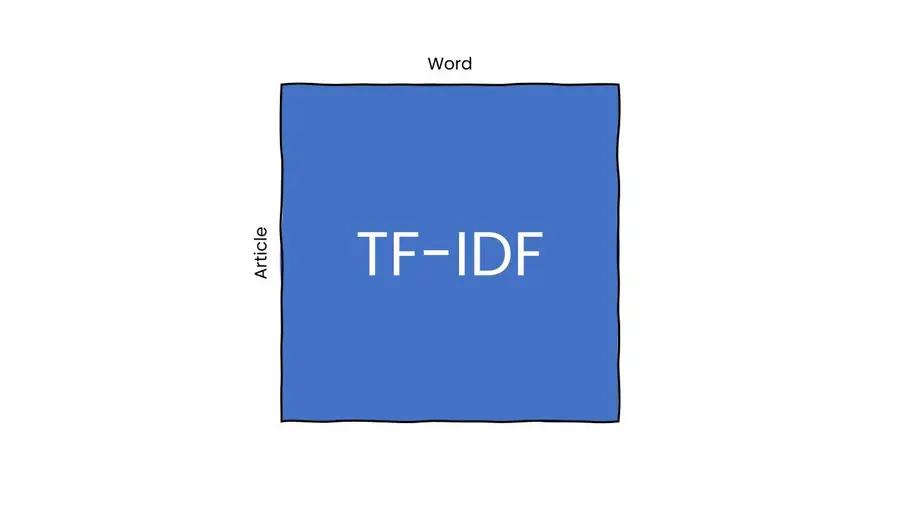
First, we take as many articles from Wikipedia as we want. This is our corpus. Second, we extract the words in each article. Third, we filter out the so-called stop words, like the, a, an, in, etc. since they don’t provide much information. The unique words that we obtain make our vocabulary. So far so good. The next step is to construct the TF-IDF matrix. Each row in this matrix maps to a unique article in our corpus while each column in this matrix maps to a unique word in our vocabulary.

For each cell in the matrix, we calculate two numbers: 1. how many times a word appears in an article (this is the term frequency or TF) and 2. how many articles a word appears in (this is document frequency or DF). We normalize the term frequency, i.e., we divide it by the total number of words in the article. We normalize the document frequency as well, i.e., we divide it by the total number of articles in our corpus. We also invert the document frequency and apply the logarithmic function to it. This is the inverse document frequency or IDF. Why do we need the IDF? Well, words that do not appear in many articles carry much more information than the ones that appear in many articles. Now, for each cell in our matrix, we divide the term frequency and the inverse document frequency. Et voila, we have our TF-IDF matrix.

This matrix does not differ much from our bag-of-words representation. So, as we said, we need to shorten it and encode some information in it. Luckily, we have our friend, linear algebra, coming to the rescue.

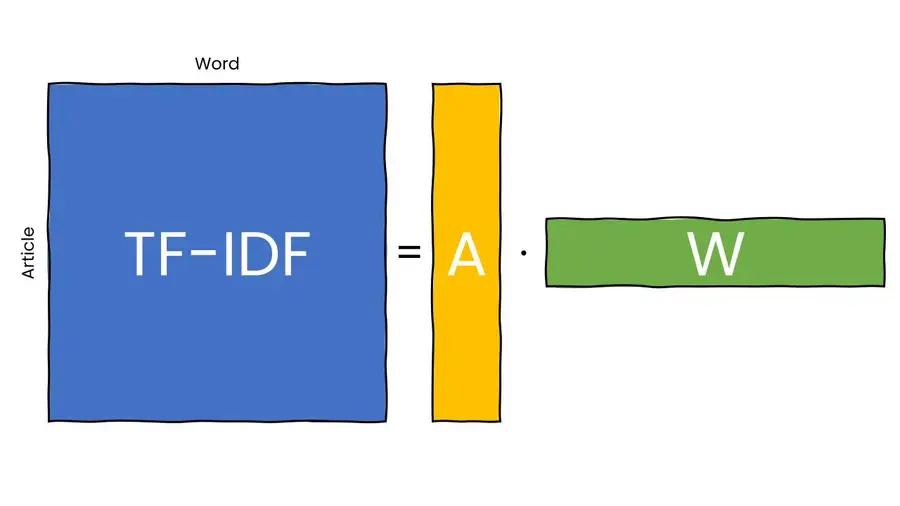
The idea is to find two rectangular matrices, one tall and narrow and the other short and wide, such that when we multiply these together we obtain the TF-IDF matrix. This is called matrix factorization. That’s it! The tall and narrow matrix have the same number of rows as the number of articles in our corpus. Each row is a representation of each article. The short and wide matrix has the same number of columns as words in our vocabulary. Each column is a representation of each word. The representation we obtain this way encodes the information we want!

Also, the width of the first matrix and the height of the second matrix are the same and the dimension is usually much much smaller than our bag-of-words representation. This factorization is obtained by a procedure called Singular Value Decomposition or SVD. Constructing the TF-IDF matrix and executing SVD on it is called Latent Semantic Analysis, or LSA. By the way, a similar procedure made one guy a millionaire by winning a Netflix competition. So, take your math classes more seriously.

“I just don’t understand how that is even possible.”— you utter. The reason why this is possible is because of how factorization works. What factorization basically does is project the points from high dimensional space to low dimensional space that satisfy the properties we want. Also, the closeness property is enforced by using the TF-IDF matrix instead of another one.

We have one problem though. Consider these two sentences:

Symphony is a culture-driven technology house.

and

Symphony is an extended musical composition for orchestra.

Did you spot the problem? With our approach above, the word Symphony will have the same representation even though its meaning in the two sentences differs.

What about context?

You probably noticed that LSA generates representations only once. We can then use them to solve the problem at hand. However, we can generate representations dynamically. This dynamic generation of representations for words will use the larger context in which the word appears. It all boils down to a simple idea: we let words attend to other words in the context. Consider the following sentence:

The chicken did not cross the road because it was too scared.

What does it refer to? Does it refer to the chicken or the road? You, as a human probably find this question trivial but for a computer, who, by the way, is dumb, this question is really hard to answer. Well, the Attention mechanism solves this problem. Several transformations down the road and we can again ask the model the same question: What does it refer to? Hopefully, it won’t answer the road.

This Attention mechanism is implemented in a class of models called the Transformers. These models are not so difficult to understand. They have a sentence as input and produce representations for each word separately. The sentence gets processed by a stack of layers who each implement the Attention mechanism. Each layer is responsible for detangling the meaning of the sentence, and figuring out the relationships between words. In the end, the meaning of each word is encoded in the representation. Magic!

If you want to read more about the Transformer and how its variants relate to each other, check out my Medium blog on this subject.

“Sooo much information!”— you shout. I know. I know. But, hopefully, it gives you a perspective of why we do the things we do. As an interdisciplinary topic, machine learning is really cool if you know how to use it. I’m afraid to ask, but…are you interested to hear more? “Well, kind of.”

About the author

Mladen Korunoski is a data scientist working at our engineering hub in Skopje.

Mladen's main interests are Machine Learning and Software Development. In software development, Mladen is versed in multiple programming languages and frameworks. In machine learning, most of his experience is in Natural Language Processing (NLP).